Paper Note - Communication-Efficient Learning of Deep Networks from Decentralized Data

01 Mar 2023

Introduction

由于毕设题目是做FL+DP方向，在这方面我真的是纯纯零基础orz，所以开始学习联邦学习和差分隐私，并且打算记录一下。

在此我真的强烈安利王树森老师这个入门视频，清晰又搞笑，看完基本可以认识到联邦学习的特点以及研究方向。从这个视频中可以了解到联邦学习有3个很重要的特质：看重隐私保护，数据不是独立同分布，通信代价大。从这几个特质中衍生出下面几个研究方向：

Communication-efficient algorithms.
Defense against privacy leakage.
Robustness to Byzantine faults.

Motivation

Communication-Efficient Learning of Deep Networks from Decentralized Data是联邦学习的开山之作，这是谷歌出于想要利用移动设备中的隐私数据训练模型而提出的。联邦学习是一种分布式机器学习，但是出于隐私保护的考虑，client对本地的数据有绝对的控制权，本地数据不会上传到server，类比于松散的联邦统治，联邦学习由此而得名。

上面提到联邦学习有以下几个特点：

看重隐私保护。
数据不是独立同分布。
通信代价大。

第1点带来了预防联邦学习隐私泄露的研究方向，比如差分隐私。第2点需要联邦学习的优化算法要在不是独立同分布的数据上work，这也对很多传统的分布式机器学习方向提出了新的问题，比如如何预防拜占庭错误。第3点成为了联邦学习算法的重要metric，在模型达到同样精度的条件下，需要通信次数越少的算法越好。

这篇文章主要解决2、3，也就是提出一种FedAvg算法，通过增大每轮通信之间的计算量，来减少通信次数，也就是Trade computation for communication，然后通过实验验证FedAvg可以用在非独立同分布的数据上。具体来说探究了两种增大计算量的思路：

在两次通信之间，增大参与计算的client数量；
增大每个client的计算量；

Method

这篇文章的baseline是large-batch synchronous SGD。具体来说，在联邦学习的setting里，就是每一轮通信，选择比例为C的client，这些client计算本地数据的损失的梯度，然后把梯度通过通信，传给server，更新模型。假设client $k$有$n_k$个数据点，计算的梯度为 $g_k$，那么更新的公式就是：

\[w_{t+1} \leftarrow w_t - \eta\sum_{k=1}^K \frac{n_k}{n}g_k\]

等价于：

\[w^k_{t+1} \leftarrow w^k_{t} - \eta g_k \\ w_{t+1} \leftarrow \sum_{k=1}^K\frac{n_k}{n}w_{t+1}^k\]

其中上标 $k$ 表示这个权重是client $k$ 本地的权重，这个式子只要留意 $w_t^k = w_t$ 就可以轻松得到。

作者把这种，每一轮通信中，每个client在用本地数据对模型进行一步梯度更新，然后server对这些client更新后的模型权重进行加权平均得到新的权重的做法称为FedSGD。上面第2种数学表达形式，把每轮通信的计算分成了两个部分，一个是client的本地更新，一个是server对于每个client更新后模型的加权平均。

在FedSGD基础上，为了增加每轮通信的计算量，可以增大每轮通信参与计算的client比例C，或者增加每个client本地的计算量，也就是增加client本地更新的次数。具体来说，可以把每个client的本地更新都当成一次独立的模型训练，client的本地更新有两个参数可调，一个是每轮通信中client本地训练的epoch数E，一个是batch size大小B。每轮通信中client的本地更新次数就可以写成 $u_k = E\frac{n_k}{B}$。这样让C、B、E可调，就得到了FedAvg算法(在FedSGD中B固定为本地的数据集大小，记为 $+\infty$，E固定为1，只有用C来调节整个算法的batch size)。

可能是怕整个算法看上去太像直接对在不同数据上分别训练的模型进行平均，所以特地做了这个图来解释了实际上，使用相同的初始化，进行模型平均能取得很好的效果。FedAvg就相当于这种相同初始化条件下的模型平均。

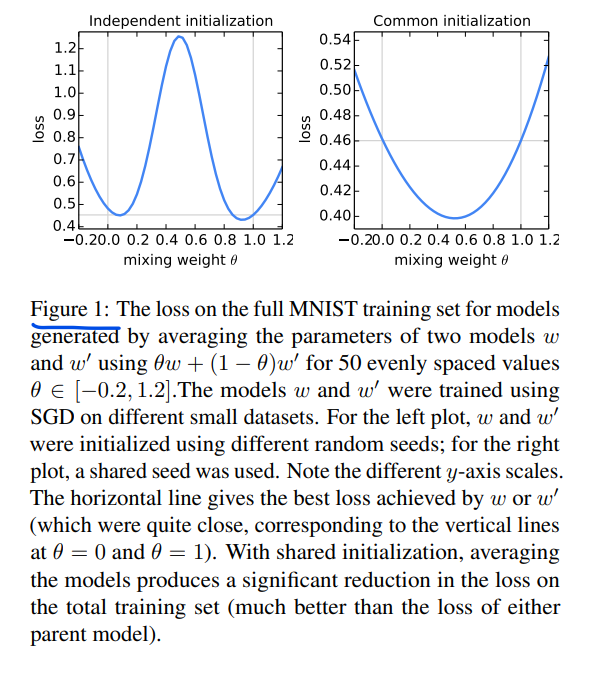
Experiment

一些实验结果。

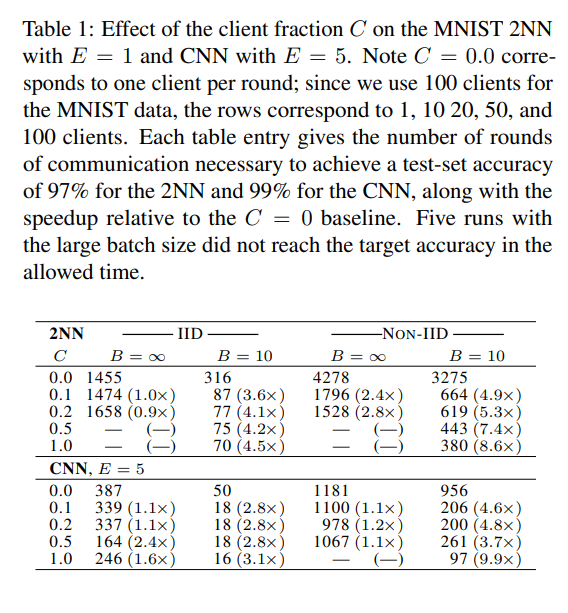
控制B、E相同，调C：

控制C相同，调不同的B、E：

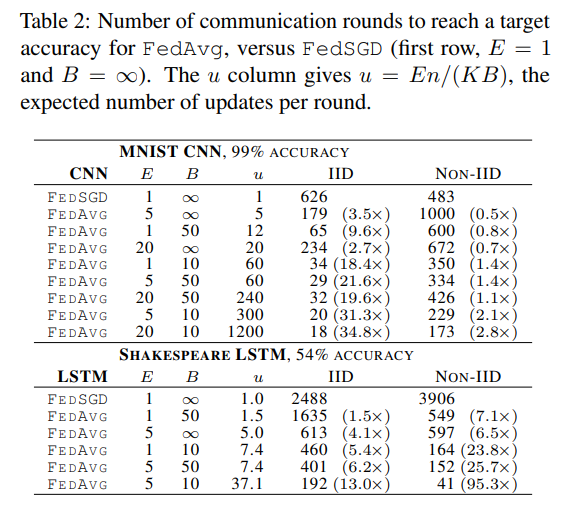
其实只要保证B大到可以充分利用移动设备硬件提供的并行度，那么减少B在增加本地更新次数的同时，是不会增加额外计算时间的。

作者还猜测这样做model averaging可以有regularization的效果，不过还有待商榷。

References

https://www.bilibili.com/video/BV1YK4y1G7jw?p=7
https://proceedings.mlr.press/v54/mcmahan17a/mcmahan17a.pdf

Qianru Lao Blogs